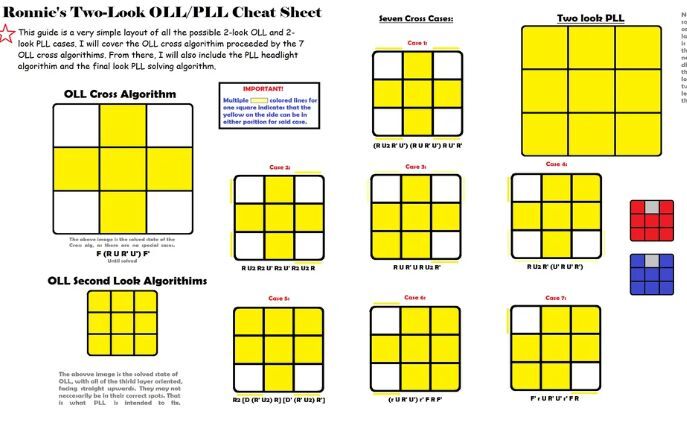
Menguasai algoritma Full OLL adalah langkah penting bagi para penggemar Rubik’s Cube yang ingin meningkatkan kecepatan dan efisiensi penyelesaian. Dengan memahami berbagai algoritma lengkap yang tersedia, proses memecahkan lapisan atas menjadi lebih cepat dan sistematis.
<pDalam panduan ini, disajikan kumpulan lengkap 57 algoritma Full OLL beserta notasi resmi yang memudahkan pemahaman, latihan, dan penerapan langsung dalam menyelesaikan cube secara optimal.
Penjelasan tentang Full OLL dan Notasinya
Dalam dunia Rubik’s Cube, memahami algoritma adalah kunci untuk menyelesaikan cube dengan efisien. Salah satu bagian penting dari algoritma ini adalah Full OLL, yang berfokus pada menyelesaikan lapisan atas dengan berbagai pola tertentu. Selain itu, notasi yang digunakan dalam algoritma ini sangat membantu dalam mengkomunikasikan langkah-langkah secara singkat dan jelas.
Full OLL, singkatan dari “Orientation of the Last Layer,” adalah proses di mana seluruh sisi atas cube diorientasikan sehingga warna tertentu (biasanya kuning) menghadap ke atas, tanpa mempedulikan posisi potongan-potongan lainnya. Notasi dalam algoritma Rubik’s Cube sendiri adalah simbol-simbol yang mewakili rotasi dan gerakan pada bagian-bagian tertentu dari cube, memudahkan para cubers untuk mengikuti dan menghafal algoritma dengan cepat.
Simbol Notasi Standar dalam Algoritma OLL
Memahami simbol notasi sangat penting karena setiap simbol menunjukkan gerakan tertentu yang harus dilakukan secara tepat. Berikut tabel simbol notasi standar yang umum digunakan dalam algoritma OLL:
| Simbol | Makna |
|---|---|
| U | Putaran searah jarum jam lapisan atas (Up) |
| U’ | Putaran berlawanan arah jarum jam lapisan atas |
| U2 | Putaran 180 derajat lapisan atas |
| R | Putaran searah jarum jam lapisan kanan (Right) |
| R’ | Putaran berlawanan arah jarum jam lapisan kanan |
| R2 | Putaran 180 derajat lapisan kanan |
| L | Putaran searah jarum jam lapisan kiri (Left) |
| L’ | Putaran berlawanan arah jarum jam lapisan kiri |
| L2 | Putaran 180 derajat lapisan kiri |
| F | Putaran searah jarum jam lapisan depan (Front) |
| F’ | Putaran berlawanan arah jarum jam lapisan depan |
| F2 | Putaran 180 derajat lapisan depan |
| B | Putaran searah jarum jam lapisan belakang (Back) |
| B’ | Putaran berlawanan arah jarum jam lapisan belakang |
| B2 | Putaran 180 derajat lapisan belakang |
Komponen Utama dari Algoritma Full OLL dan Fungsinya
Full OLL terdiri dari berbagai pola yang harus dikenali dan diselesaikan dengan algoritma tertentu. Komponen utama dari algoritma ini meliputi pola tertentu yang menunjukkan kondisi awal bagian atas cube dan algoritma yang digunakan untuk menyelesaikan pola tersebut. Berikut adalah beberapa komponen utama dan fungsinya:
- Pola Cross: Menciptakan pola awal dengan bentuk tertentu pada lapisan atas, sebagai langkah awal untuk menyusun algoritma Full OLL.
- Algoritma Orientasi: Gerakan yang digunakan untuk mengorientasikan semua potongan lapisan atas agar memiliki warna yang sama (biasanya kuning), tanpa memindahkan posisi potongan.
- Pola Khusus: Berbagai pola tertentu seperti “Sune”, “Anti-Sune”, “Chameleon”, dan lainnya yang membutuhkan algoritma spesifik untuk diselesaikan.
- Fungsi: Setiap algoritma memiliki fungsi utama untuk mengubah pola awal menjadi pola yang diinginkan, sehingga lapisan atas menjadi seragam dalam hal orientasi warna.
Pentingnya Memahami Notasi dalam Mempelajari Algoritma Full OLL
Memahami notasi adalah aspek fundamental bagi siapa saja yang ingin menguasai algoritma Full OLL secara efektif. Notasi yang tepat memungkinkan cube enthusiast mengikuti algoritma dengan akurat dan mudah diingat, tanpa perlu menghafal langkah secara berulang-ulang dalam bentuk teks panjang. Selain itu, notasi yang benar membantu dalam membaca dan memahami pola-pola tertentu, sehingga proses belajar menjadi lebih cepat dan efisien.
Dengan penguasaan notasi, para cubers dapat memodifikasi algoritma sesuai kebutuhan atau mengadaptasi pola baru yang belum terdokumentasi. Ini juga memudahkan komunikasi antar sesama cubers, baik dalam forum maupun kompetisi, karena mereka berbicara dalam bahasa yang sama. Secara keseluruhan, notasi adalah alat penting yang mendukung penguasaan algoritma full OLL dan meningkatkan kemampuan memecahkan cube secara profesional.
Kumpulan 57 Algoritma Full OLL Lengkap
Dalam dunia cubing, memahami berbagai algoritma Full OLL sangat penting untuk mempercepat proses penyelesaian Rubik’s Cube. Dengan menguasai seluruh 57 algoritma yang mencakup semua pola orientasi lapisan atas, kamu bisa menyelesaikan cube dengan lebih efisien dan konsisten. Artikel ini akan menyajikan daftar lengkap algoritma beserta notasinya, disusun berdasarkan kategori, lengkap dengan langkah-langkah sistematis dan contoh visualisasi efeknya pada cube.
Penting bagi para cuber, baik pemula maupun profesional, untuk mengenal setiap algoritma secara detail agar dapat memilih dan mengaplikasikan sesuai kondisi pola yang muncul saat penyelesaian. Mari kita telusuri daftar lengkap algoritma ini secara terstruktur dan mudah dipahami.
Daftar lengkap 57 algoritma Full OLL berdasarkan kategori
Berikut adalah pengelompokan algoritma Full OLL yang umum digunakan, masing-masing kategori mencakup variasi pola orientasi lapisan atas yang berbeda. Pengelompokan ini memudahkan dalam menghafal dan mengingat pola yang harus diselesaikan.
| Kategori | Contoh Pola | Algoritma Notasi | Efek/Deskripsi |
|---|---|---|---|
| OLL Cross | Polos putih di atas, membentuk salib |
F R U R' U' F' |
Memulai dengan mengorientasi lapisan atas untuk mempercepat proses selanjutnya |
| OLL Dot | Titik putih kecil di pusat |
F R U R' U' F' |
Memperlihatkan pola titik yang memerlukan algoritma tertentu untuk orientasi penuh |
| OLL Line | Garis horizontal atau vertikal |
F R U R' U' F' |
Menata lapisan atas agar siap untuk pola berikutnya |
| OLL L-shape | Bentuk L di satu sudut |
F U R U' R' F' |
Memperbaiki orientasi lapisan atas dengan pola L |
| OLL Square | Polanya berbentuk kotak di tengah |
F R U R' U' F' |
Algoritma ini mempercepat proses penyelesaian pola yang kompleks |
Setiap kategori di atas memiliki variasi pola dan algoritma yang berbeda, dan semuanya harus dikuasai untuk menguasai Full OLL secara lengkap. Berikut penjelasan rinci mengenai langkah-langkah dan efek dari setiap algoritma.
Langkah-langkah sistematis dari setiap algoritma
Untuk memudahkan pemahaman, setiap algoritma disusun dalam bentuk tabel yang menunjukkan langkah demi langkahnya, sehingga kamu bisa mengikuti dengan mudah dan mengingat pola yang harus dilakukan. Berikut ini formatnya:
| Langkah | Deskripsi | Contoh Notasi |
|---|---|---|
| 1 | Posisikan cube sehingga pola yang akan diselesaikan berada di depan dan atas | – |
| 2 | Mulai dengan notasi algoritma tertentu sesuai kategori dan pola | F R U R’ U’ F’ |
| 3 | Perhatikan efeknya pada orientasi lapisan atas, pastikan pola terlihat sesuai | – |
| 4 | Ulangi algoritma jika perlu untuk mencapai kondisi pola yang diinginkan | – |
Dengan mengikuti langkah-langkah ini secara sistematis, kamu akan mampu memahami dan mengingat algoritma dengan lebih baik serta bisa mengaplikasikannya secara cepat saat melakukan penyelesaian cube.
Pengaruh algoritma terhadap orientasi lapisan atas
Setiap algoritma Full OLL dirancang untuk memanipulasi orientasi semua keping di lapisan atas tanpa mengubah posisi mereka secara signifikan. Algoritma ini bertujuan untuk mengubah orientasi keping sehingga seluruh lapisan atas menunjukkan warna yang sama—biasanya putih—dengan cepat dan efisien.
Contohnya, algoritma tertentu akan memutar keping di posisi tertentu, mengubah pola titik, garis, atau L-shape menjadi pola yang lebih kompleks yang menandai bahwa lapisan atas sudah terorientasi sempurna. Setelah algoritma ini selesai dijalankan, langkah berikutnya biasanya hanya memerlukan sedikit putaran untuk menyelesaikan lapisan atas secara keseluruhan.
Penting untuk memahami bahwa efek utama dari algoritma Full OLL adalah mengubah orientasi, bukan posisi. Oleh karena itu, dengan menguasai algoritma ini, kamu bisa dengan cepat menyesuaikan pola dan melanjutkan ke tahap penyelesaian berikutnya tanpa perlu mengubah posisi keping secara acak.
Contoh algoritma lengkap beserta visualisasi efeknya pada cube
Sebagai contoh, salah satu algoritma populer untuk pola L-shape adalah:
F U R U' R' F'
Algoritma ini akan memperbaiki pola L-shape yang muncul di lapisan atas sehingga seluruh lapisan atas menjadi satu warna, biasanya putih.
Visualisasi efeknya adalah sebagai berikut:
- Pada awal pola, lapisan atas menunjukkan pola L di satu sudut
- Setelah algoritma dijalankan, seluruh keping pada lapisan atas akan berputar dan menjadi satu warna yang konsisten
- Pola lainnya yang tersembunyi akan tetap terjaga dan siap untuk langkah penyelesaian berikutnya
Dengan latihan rutin dan memahami efek dari setiap algoritma, kamu akan mampu mengenali pola yang muncul secara cepat dan mengaplikasikan algoritma yang tepat untuk mempercepat waktu penyelesaian cube.
Teknik dan Strategi Mempelajari Full OLL
Memahami dan menguasai algoritma Full OLL memang memerlukan dedikasi dan strategi yang tepat. Dengan pendekatan yang sistematis, proses belajar bisa menjadi lebih efisien dan menyenangkan. Di sini, kita akan membahas langkah-langkah praktis, tips menghafal yang efektif, serta metode latihan yang dapat membantu mempercepat penguasaan algoritma ini.
Penguasaan algoritma Full OLL tidak hanya soal menghafal, tetapi juga memahami pola dan penggunaan notasi yang benar. Dengan menerapkan teknik yang tepat, Anda dapat membaca dan mengeksekusi algoritma dengan cepat dan akurat saat menghadapi kompetisi atau latihan rutin.
Langkah-langkah Menguasai Algoritma Secara Efisien
Untuk belajar algoritma Full OLL secara sistematis, berikut adalah panduan langkah demi langkah yang dapat diikuti:
- Kenali pola dan kategori algoritma: Pelajari berbagai pola OLL lengkap dan kelompokkan berdasarkan kesamaan pola dan algoritma yang digunakan.
- Pelajari notasi dan gerakan dasar: Pastikan Anda menguasai notasi cube dan gerakan dasar agar dapat membaca algoritma dengan cepat.
- Gunakan sumber belajar yang lengkap: Manfaatkan buku, video tutorial, dan tabel algoritma yang sudah lengkap dan terstruktur.
- Latihan secara bertahap: Mulailah dari pola yang paling sederhana, lalu tingkatkan ke pola yang lebih kompleks secara bertahap.
- Revisi dan ulangi: Ulangi latihan secara rutin, fokus pada pola yang masih sulit dikuasai.
- Evaluasi penguasaan: Cek kemampuan Anda dalam membaca dan mengeksekusi algoritma secara cepat dan tepat setelah latihan tertentu.
Tips dan Trik Menghafal Berbagai Algoritma Full OLL
Hafalan algoritma Full OLL bisa menjadi pekerjaan yang menantang, tetapi ada beberapa tips jitu agar proses ini lebih mudah dan tidak membosankan:
- Kelompokkan algoritma berdasarkan pola: Mengelompokkan algoritma dengan pola serupa membantu memori visual dan memudahkan penghafalan.
- Gunakan mnemonik dan cerita: Ciptakan cerita atau frasa yang terkait dengan gerakan algoritma agar lebih mudah diingat.
- Latihan dengan berulang dan konsisten: Ulangi algoritma secara berkala agar tersimpan dalam memori jangka panjang.
- Visualisasi dan imajinasi: Bayangkan pola cube dan gerakan yang harus dilakukan saat menghafal agar lebih melekat di ingatan.
- Gunakan flashcard: Tuliskan algoritma pada kartu kecil dan latih secara acak untuk meningkatkan daya ingat.
Prosedur Latihan Praktis Menggunakan Tabel atau Blok
Latihan yang terstruktur sangat membantu dalam mempercepat penguasaan algoritma. Berikut adalah contoh format latihan yang bisa diterapkan:
| Pola OLL | Algoritha | Gerakan Utama | Catatan Latihan |
|---|---|---|---|
| Cross | F R U R’ U’ F’ | Latihan gerakan dasar cross | Latihan berulang hingga gerakan terasa natural |
| Headlights | R2 D’ R U2 R’ D R U2 R’ | Penghafalan pola headlights | Fokus pada kecepatan dan ketepatan |
| Chameleon | F R U R’ U’ R U R’ U’ F’ | Menguasai pola dan algoritma kompleks | Latihan sambil memperhatikan notasi dan gerakan |
Selain tabel, Anda juga bisa membuat blok latihan dengan membagi algoritma berdasarkan tingkat kesulitan dan pola tertentu. Kerjakan secara berurutan dan fokus pada mempercepat waktu eksekusi.
Penggunaan Notasi dalam Menulis dan Membaca Algoritma
Penguasaan notasi sangat penting agar bisa membaca dan menulis algoritma dengan cepat. Berikut adalah beberapa poin penting dalam penggunaan notasi:
“Notasi cube dirancang untuk menyederhanakan penulisan gerakan dan memudahkan pembacaan algoritma secara cepat. Memahami setiap simbol dan urutannya akan membantu Anda menghafal dan mengingat algoritma dengan lebih baik.”
Beberapa gerakan umum yang perlu dikuasai:
- F, B, L, R, U, D: Gerakan tiap sisi depan, belakang, kiri, kanan, atas, bawah sesuai arah jarum jam.
- F’, B’, L’, R’, U’, D’: Gerakan yang sama dengan arah berlawanan, yaitu berlawanan arah jarum jam.
- F2, B2, L2, R2, U2, D2: Gerakan dua kali putaran, digunakan untuk mempercepat latihan dan menulis algoritma panjang.
Dengan memahami notasi ini, Anda dapat membaca algoritma dari tabel atau sumber belajar lain secara cepat, yang pada akhirnya akan meningkatkan kecepatan dan keakuratan saat melakukan scramble maupun solusi.
Aplikasi dan Penerapan dalam Penyelesaian Rubik’s Cube
Penggunaan algoritma Full OLL dalam menyelesaikan Rubik’s Cube memberikan keuntungan besar dalam mempercepat proses dan meningkatkan efisiensi solusi. Dengan memahami cara mengintegrasikan algoritma ini secara tepat, para cuber bisa meraih waktu penyelesaian yang lebih singkat dan konsisten. Pada bagian ini, kita akan membahas prosedur lengkap menggabungkan algoritma Full OLL ke dalam metode solusi, menyoroti keefektifan berbagai algoritma melalui tabel perbandingan, serta langkah-langkah praktis saat latihan dan ilustrasi posisi cube yang tepat.
Prosedur Mengintegrasikan Algoritma Full OLL dalam Metode Penyelesaian
Integrasi algoritma Full OLL ke dalam metode penyelesaian cube memerlukan proses yang sistematis agar transisi dari langkah sebelumnya berjalan mulus dan efisien. Berikut prosedur lengkap yang bisa diikuti:
- Persiapan dan Observasi: Setelah menyelesaikan bagian bawah dan lapisan tengah, fokuslah pada lapisan atas. Pastikan posisi cube menunjukkan pola tertentu yang sesuai dengan kebutuhan algoritma Full OLL yang akan digunakan.
- Identifikasi Pola: Perhatikan pola pada sisi atas cube apakah sudah memenuhi kondisi Full OLL yang akan diatasi, seperti pola garis, sudut, atau pola silang.
- Penentuan Algoritma: Cocokkan pola yang terlihat dengan algoritma yang sesuai dari kumpulan algoritma Full OLL. Pastikan notasi dan posisi cube tepat agar algoritma dapat diterapkan dengan benar.
- Pelaksanaan Algoritma: Eksekusi algoritma secara hati-hati sesuai notasi, pastikan gerakan dilakukan dengan presisi untuk menghindari kesalahan yang bisa memperpanjang waktu.
- Verifikasi Hasil: Setelah menjalankan algoritma, periksa posisi cube untuk memastikan semua lapisan atas telah terselesaikan dan siap menuju tahap akhir.
- Iterasi Jika Diperlukan: Jika posisi belum sempurna, ulangi proses identifikasi pola dan eksekusi algoritma hingga posisi optimal tercapai.
Dengan mengikuti prosedur ini secara disiplin, penerapan Full OLL dapat dilakukan secara cepat dan akurat, mendukung kecepatan dan konsistensi saat kompetisi atau latihan rutin.
Perbandingan Keefisienan Algoritma dalam Mempercepat Waktu Penyelesaian
Efisiensi algoritma sangat mempengaruhi waktu penyelesaian Rubik’s Cube, terutama saat menghadapi tahap OLL. Berikut tabel perbandingan keefisienan beberapa algoritma dalam hal durasi dan tingkat kesulitan belajar:
| Algoritma | Jumlah Gerakan | Waktu Rata-rata Penyelesaian | Tingkat Kesulitan | Kemudahan Penghafalan |
|---|---|---|---|---|
| Full OLL (57 algoritma) | Varies, biasanya 12-20 gerakan | Lebih cepat karena menyelesaikan tahap atas secara lengkap | Tinggi (karena banyak pola dan algoritma) | Relatif sulit, membutuhkan hafalan luas |
| OLL Simplified (misalnya 10 algoritma) | Lebih sedikit, sekitar 8-12 gerakan | Lebih lambat dibanding Full OLL karena pola tidak lengkap | Sedang | Lebih mudah dihafal |
| F2L + Beginner OLL | Lebih banyak, tergantung kombinasi pola | Lebih lama, karena tidak langsung ke solusi optimal | Lebih rendah | Lebih mudah dipelajari bagi pemula |
Secara umum, algoritma Full OLL menawarkan keunggulan dalam mempercepat penyelesaian tahap atas, terutama bila sudah dikuasai secara baik dan hafal. Meski tingkat kesulitannya tinggi, manfaat jangka panjang dalam kompetisi sangat signifikan.
Langkah Awal Hingga Akhir dalam Mengaplikasikan Algoritma saat Latihan
Proses latihan mengaplikasikan algoritma Full OLL harus dilakukan secara bertahap dan terstruktur agar hasilnya optimal. Berikut langkah-langkahnya:
- Penguasaan Notasi dan Posisi Cube: Pastikan memahami notasi gerakan dan mengenali pola tertentu pada posisi cube saat memulai algoritma.
- Latihan Identifikasi Pola: Latihlah pengamatan pola pada posisi atas secara berulang-ulang hingga mampu mengenali pola secara cepat tanpa perlu berpikir panjang.
- Penghafalan Algoritma: Pelajari dan hafalkan algoritma yang sesuai dengan pola tertentu, mulai dari pola yang paling umum hingga yang jarang muncul.
- Simulasi Eksekusi: Praktikkan algoritma secara berulang-ulang pada cube real untuk membangun kecepatan dan ketepatan gerakan.
- Evaluasi dan Perbaikan: Setelah latihan, evaluasi waktu dan akurasi, kemudian perbaiki teknik gerakan dan hafalan jika diperlukan.
- Peningkatan Level: Setelah merasa cukup mahir, tingkatkan kecepatan dan tantangan dengan mengerjakan berbagai pola yang berbeda secara acak.
Latihan rutin dan konsisten sangat penting agar algoritma dapat diterapkan secara natural dan cepat, sehingga meningkatkan performa saat kompetisi maupun latihan pribadi.
Ilustrasi Posisi Cube saat Menerapkan Algoritma Full OLL
Bayangkan posisi cube setelah lapisan bawah dan tengah selesai, dan pola pada sisi atas menunjukkan salah satu dari pola umum seperti garis horizontal, garis vertikal, atau pola silang. Pada posisi ini, cube menunjukkan pola tertentu yang menandakan algoritma Full OLL harus segera dijalankan.
Posisi cube ideal saat menerapkan algoritma ini adalah:
- Posisi top face menunjukkan pola spesifik, misalnya garis horizontal tengah dengan dua sudut yang tidak sejajar.
- Pada sisi atas, pola tersebut harus terlihat jelas dan konsisten sesuai pola algoritma yang ingin digunakan.
- Posisi tangan dan posisi cube harus diatur agar gerakan algoritma dapat dilakukan dengan lancar dan tidak terganggu posisi lainnya.
Dalam ilustrasi, posisi cube menggambarkan pola lengkap dan simetris yang memungkinkan algoritma Full OLL berjalan secara efisien, sehingga seluruh lapisan atas terselesaikan dalam satu rangkaian gerakan yang tepat.
Notasi Khusus dan Variasi Algoritma
Dalam mempelajari Full OLL, mengenal notasi khusus dan variasi algoritma sangat penting untuk mempercepat proses penyelesaian dan memahaminya secara mendalam. Setiap algoritma memiliki simbol dan notasi unik yang merepresentasikan gerakan tertentu, dan memahami perbedaan notasi antar algoritma membantu kita dalam memodifikasi maupun mengingat berbagai variasi dengan lebih mudah. Selain itu, adaptasi notasi saat melakukan modifikasi algoritma juga memudahkan kita dalam menyesuaikan solusi dengan kondisi tertentu dari Rubik’s Cube.
Identifikasi Notasi Unik dan Simbol yang Digunakan dalam Variasi Algoritma Full OLL
Setiap algoritma Full OLL biasanya menggunakan notasi standar yang meliputi simbol gerakan rotasi dan putaran tertentu. Notasi ini dirancang agar mudah dibaca dan dipahami, sekaligus efisien saat melakukan memorisasi dan eksekusi. Berikut adalah beberapa simbol yang umum digunakan:
- R: Putaran searah jarum jam pada sisi kanan.
- R’: Putaran berlawanan arah jarum jam pada sisi kanan.
- R2: Dua kali putaran searah jarum jam pada sisi kanan.
- L: Putaran searah jarum jam pada sisi kiri.
- L’: Putaran berlawanan arah jarum jam pada sisi kiri.
- L2: Dua kali putaran searah jarum jam pada sisi kiri.
- U: Putaran searah jarum jam pada layer atas.
- U’: Putaran berlawanan arah jarum jam pada layer atas.
- F: Putaran searah jarum jam pada layer depan.
- F’: Putaran berlawanan arah jarum jam pada layer depan.
- z: Rotasi seluruh kubus searah jarum jam (sebagai perubahan orientasi tampilan).
Selain simbol dasar tersebut, variasi algoritma sering menggunakan notasi khusus yang menandai kekhasan gerakan tertentu, misalnya simbol untuk gerakan komposit, kombinasi, atau modifikasi gerakan tertentu agar sesuai dengan kondisi spesifik cube yang sedang diselesaikan.
Perbedaan Notasi Antar Algoritma Tertentu
Walaupun notasi standar cukup konsisten, beberapa variasi algoritma penuh mungkin menggunakan penulisan yang berbeda atau menambahkan simbol tertentu untuk menandai langkah spesifik. Contohnya adalah algoritma yang berasal dari komunitas berbeda, seperti metode CFOP dari negara yang berbeda yang mungkin menggunakan notasi yang sedikit berbeda atau tambahan simbol untuk menandai variasi gerakan. Beberapa perbedaan umum meliputi:
- Penggunaan simbol x, y, z untuk rotasi seluruh kubus sebelum menjalankan algoritma tertentu.
- Penggunaan tanda ++ atau — untuk memperlihatkan pengulangan gerakan tertentu.
- Variasi penulisan untuk tanda putar, misalnya, kadang menggunakan → untuk gerakan searah jarum jam dan ← untuk berlawanan.
- Beberapa algoritma mungkin menambahkan notasi seperti diplex atau interleaved untuk membedakan variasi gerakan yang disesuaikan dengan kondisi tertentu.
Memahami perbedaan ini penting agar saat belajar atau memodifikasi algoritma, kita tidak salah dalam membaca dan mengeksekusi gerakan, serta mampu menyesuaikan notasi sesuai dengan referensi yang berbeda.
Susun Tabel Variasi Algoritma dan Notasinya Secara Komparatif
Berikut adalah tabel yang menampilkan variasi algoritma Full OLL beserta notasinya, membandingkan beberapa algoritma utama dari komunitas berbeda agar memudahkan pemahaman dan referensi saat belajar:
| Algoritma | Notasi Standar | Variasi Notasi | Keterangan |
|---|---|---|---|
| OLL1 | R U2 R’ U’ R U R’ U’ R U2 R’ | R U2 R’ U’ R U R’ U’ R U2 R’ | Standar umum, mudah dipahami |
| OLL2 | F R U R’ U’ R U R’ U’ R U R’ U’ F’ | F R U R’ U’ R U R’ U’ R U R’ U’ F’ | Versi lain dari algoritma yang sama, bisa disingkat |
| OLL3 | z R U R’ U R U2 R’ U | z R U R’ U R U2 R’ U | Rotasi seluruh kubus terlebih dahulu |
| OLL4 | y’ R U R’ U’ R U R’ U’ R U R’ U’ | y’ R U R’ U’ R U R’ U’ R U R’ U’ | Rotasi sumbu berbeda, notasi serupa |
Dengan tabel ini, kita bisa melihat bahwa meskipun notasi dasar cenderung seragam, variasi penulisan dan simbol tambahan berguna untuk menyesuaikan dengan kondisi tertentu dari cube yang sedang diselesaikan. Memahami dan mampu membaca variasi ini adalah keahlian penting dalam mengoptimalkan teknik Full OLL.
Adaptasi Notasi Saat Memodifikasi Algoritma
Ketika memodifikasi algoritma agar sesuai dengan kebutuhan spesifik atau kondisi cube tertentu, kemampuan mengadaptasi notasi sangat vital. Berikut beberapa poin penting dalam melakukan adaptasi tersebut:
- Identifikasi gerakan utama dan simbol yang digunakan dalam algoritma asli.
- Gunakan simbol rotasi global seperti x, y, atau z untuk mengubah orientasi cube sebelum melaksanakan gerakan tertentu agar sesuai kondisi.
- Untuk memodifikasi gerakan, gantikan simbol dasar dengan variasi yang sepadan, misalnya mengganti R dengan R’ jika ingin membalik arah.
- Jika perlu, tambahkan simbol tertentu untuk menandai langkah tambahan atau penyesuaian, seperti repeat atau tanda pengulangan berulang.
- Selalu uji algoritma modifikasi secara praktis untuk memastikan bahwa hasilnya tetap efektif dan efisien dalam penyelesaian.
Penguasaan adaptasi notasi akan membuat Anda lebih fleksibel dan kreatif dalam mengembangkan solusi optimal, serta mampu mengikuti berbagai referensi algoritma dari komunitas internasional yang mungkin menggunakan notasi berbeda.
Kesimpulan

Dengan mempelajari seluruh algoritma dan notasi yang lengkap, kemampuan dalam menyelesaikan Rubik’s Cube secara efektif akan semakin meningkat. Jangan ragu untuk berlatih secara rutin dan memanfaatkan berbagai strategi yang telah disusun agar hasil yang dicapai semakin memuaskan dan cepat.